- November 15, 2011
- Posted by: SebastianRiedel
- Category: Research News, Research Spotlight
Application of pore-network models in two-phase flow in porous media

By Vahid Joekar-Niasar on the occasion of his InterPore-Fraunhofer Award for Young Researchers
Compared to other pore-scale methods for simulating two-phase flow in porous media, pore-network modeling has been used more extensively, as it is relatively simple and computationally less demanding. Pore-network modeling has also its own cons and pros. While pre-processing is required to idealize the pore space geometry and topology into simplified inter-connected geometries, the significant benefit is that larger physical domains can be simulated. Other pore-scale models such as lattice Boltzmann (LB), smoothed particle hydrodynamics (SPH), and level set (LS) methods are resolution based, while pore-network model is resolution-free. When simulating flow in a domain that is physically larger than the REV1, other methods are impractical for analysis of continuum-scale theories.
- Network generation: A pore network is usually made of large pores (pore bodies) connected to each other through narrow long pores (pore throats). The topological and geometrical information can be obtained from imaging techniques to construct either a statistically-equivalent network or an exact network based on the imaged sample.
- Deriving analytical solutions: Analytical relations to define the pore-scale mechanisms for given pore geometry should be derived. For instance, for a two-phase flow problem, pore-scale flow equation, entry capillary pressure relations, and snap-off capillary pressures relation should be provided.
- Solving balance equations over the whole network: Systems of equations should be composed to solve the pressure field and calculate phase flows over the whole network.
- Averaging from pore-scale to Darcy scale: Pore-scale quantities will be averaged to obtain a Darcy-scale quantity. In our research, we focused on analysis of capillarity theories developed by Hassanizadeh and Gray, [1990]. These theories propose new physical insights that are absent in classical Darcy’s law. They proposed specific interfacial area as a new state variable that can eliminate some complexities related to the hysteresis in capillary pressure-saturation relation. Furthermore, they propose that Darcy’s law can be generalized by inclusion of gradient free energy that is related to fluid phases and interfacial area.
Quasi-static pore-network models: These models provide equilibrium saturation profiles for given boundary pressures. Three models were developed for hypothetical, 2-D micro-model, and 3-D glass bead samples to analyze the uniqueness of Pc-S-anw. The validation of the pore-network models against experiments showed the reliable applicability of these models to investigate the theory. These models cover different levels of complexity. While the hypothetical model is quite simple (having regular lattice with circular cross sections), the glass bead pore-network model is unstructured irregular with mixed hyperbolic cross sections. Thus, the relationships for entry capillary pressure, specific interfacial area, etc. had to be derived.
Moreover, the wide range of analysis illustrated how Pc-S-anw surface can change depending on pore geometry. A medium with high porosity was also simulated using quasi-static pore-network models. A medial axis transform was used to extract the topology and geometry of the porous medium and as shown in Figure 1, the drainage and imbibi-tion cycles were successfully simulated using this model.
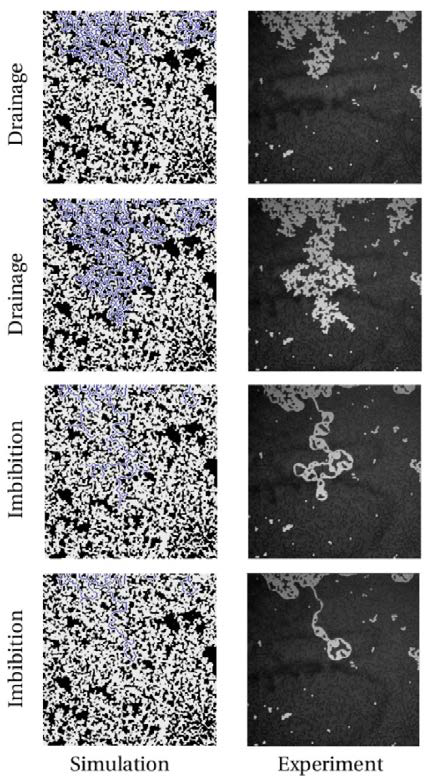
| Ca = 10-7
Ca = 10-6 |
 |
|
| Figure 2: 2-D saturation profiles at Sw=0.8 for different viscosity ratios and capillary numbers simulated by DYPOSIT |
Figure 3: 3-D saturation profile simulated using the DYPOSIT model for a capillary rise problem |
|
References
- Hassanizadeh, S. M. & Gray, W. G. 1990 Mechanics and thermodynamics of multiphase flow inporous media including interphase boundaries. Adv. Water Resour. 13, 169–186.
- Joekar-Niasar, V. 2010, The immiscibles, Utrecht University, ISBN 978-90-5744-179-0; http://www.geo.uu.nl/~wwwhydro/vahid/vahid.html
- Joekar-Niasar, V., and S. M. Hassanizadeh 2010, Effect of fluids properties on non-equilibrium capillarity effects: Dynamic pore-network modeling, Int. J. Multiphase Flow, 37, 198–214
- Joekar-Niasar, V., S. M. Hassanizadeh, and H. K. Dahle 2010, Non-equilibrium effects in capil-larity and interfacial area in two-phase flow: Dynamic pore-network modelling, J. Fluid. Mech., 655, 38–71
- Koplik, J. & Lasseter, T. J. 1985 Two-phase flow in random network models of porous me-dia.Soc. Petrol. Engng J. 25, 89–110.
1 Representative Elementary Volume
2 DYnamic POre-network SImulator for Two-phase flow
